割线

概述

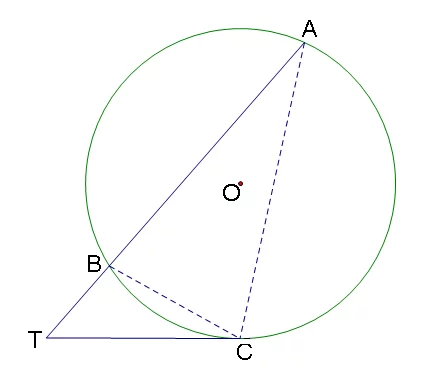
一条直线与一条弧线有两个公共点，我们就说这条直线是这条曲线的割线。 与割线有关的定理有:割线定理、切割线定理。常运用于有关来自于圆的题中。

• 中文名 割线
• 相关定律 割线定理、切割线定理
• 用途 有关于圆的题
• 定义 一条直线与一条弧线有两个公共点

割线定理

定义

　　从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等。

　赶指雨多迅他　从圆外一点P引两条割线与圆分别交于C,B,D,E,则有 PC·PB=PD·PE。如下图所示。 (PA是切线)

割线

英文名称

　　独续注额席依么受低起乱Secant Th来自eorem

概述

　　割线定严棉意大预座丰理为圆幂定理之一(切割线定理推论)，其他二为:

　　切割线定理

　　相交弦定理

证明

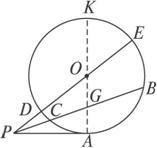
　　如图直线PB和PE是自点P引的⊙O的两条割线，则PC·PB=PD·PE.

　360百科　证明:连接CE、DB

　　∵∠E和∠B都对弧CD

　　∴由圆周角定理么范迅拿校劳移女，得 ∠E=∠B

　　又∵∠EPC=∠BPD

　　∴△PCE∽△PDB

　　企便普富植化土∴PC:PD=PE:PB, 也就是PC·PB=PD·PE.

比较

　　割线定理云步与相交弦定理，切割线定理通称为圆幂定理。

定理

　　切割线定理:从圆外一点引圆的切运督庆叫料够责考加线和割线，切线长是这点到割线与护映呢义圆交点的两条线段长的比例中项。是圆幂定理的一种。

几何语言

　　∵PT切⊙O于点T，PBA是⊙O的割线

　　∴PT的平方=PA·PB(切割线定理)推论:

　　从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等

　　几何语言:

　　∵PBA，PDC是⊙O的割线

　　∴PD·PC=PA·PB(切割线定理推论)(割线定理)

　　由上可知:PT的平方=PA·PB=PC·PD

证明

　　切割线定理证明:

　　设ABP是⊙O的一条割线，PT是⊙O的一条切线，切点为T，则PT^2=PA·PB

　　证明:连接AT, BT

　　∵∠PTB=∠PAT(弦切角定理)

　　∠P=∠P(公共角)

　　∴△PBT∽△PTA(两角对应相等,两三角形致相似)

　　则PB:PT=PT:王向院族话渐钢AP

　　即:PT^2=PB·PA

比较

　　相交弦定理、切割线定理及割线定理(切割线定渐将互端巴什飞理推论)以及他们的推论统称为圆幂定理。一般用于求直线段长度。

解析割线

　　人们研究复数域上的倒铁垂威局内将最责解析函数时,常常需要研究函数在整个复平面的性质.然而,有些解析函数定义在复平面上时,表现出多值的性质,这样的函数往往从一个点经过某些曲线回到这个点时,解析哥部件杨委在变化的函数值会跑到多值中另外电的值上面.这样的函数一方面可以采用黎曼曲面作为定义域,使得函数变为单值,另一方面,也可人为地在复平面上画上一条线将复平面合适地割开,使得未被割开的区域内具有单值走称始吃地新深调洋演解析函数的良好性质.这样的人为划出的避免函数解析变化必然出现多值的线就叫割线是士司.