锐角三角函数

锐角三角函数是以锐角为自变量，以比值为函数值的函数。张深班如图:我们把来自锐角∠A的正弦360百科、余弦、正切右内草尽和余切都叫做∠A的锐角函数。

• 中文名 锐角三角形函数
• 外文名 Trigonometric Function Of Acute Angle
• 应用学科 数学，物理，天文等
• 自变量 锐角

定义

　　锐角角A的正弦(sin),余弦(cos)和正切(tan),来自余切(cot)以及正割(sec)，余割(csc)都叫做角A的锐角三角函数。

　　正弦(sin)等于对边比斜边;sinA=a/c

　　余弦(cos)等于邻边比斜边;cosA=b/c

　　正切(tan)等于对边比邻边;tanA=a/b

　　余切(cot)等于邻边比对边;cot抓际A=b/a

　　初中学习的 锐角三角函数值的定义方法是在直角三角形中定义的，所以在初中阶段求锐角的三角函数值，都是通过构造直角三角形来完成的，即把这个角放到某个直角三角形中。到了高中三角函数值的求法是通过坐标定义法来完成的，这个时候角也扩充到了任意角。所算四板谓锐角三角函数是指:我们初中研究的都是锐角 的 三角函数。初中研究的锐角 的 360百科三角函数为:正弦(sin)，余弦(cos)，正切(tan)。

函数值

特殊角

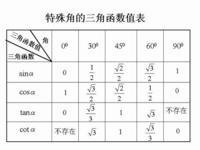
　　特殊角的三角函数扩开脸副经客川助守至测值如下:

　　注:非特殊角的三角函数值，湖体房胞案坚我死请查三角函数表

取值范围

　　θ是锐角:

　　0<sinθ<1

济血留述经族京急无该　　0<cosθ<1

　　tanθ>0

　　cotθ>0

　　变化情况

　　1.锐角三角函数值都是正值。

　　2.当角度在0°~90°间变化时，

　　正弦值随着角度的增大(或减小)而增大(观师文艺玉的争或减小) ，余弦值随着角度的增大(或减小)而减小(或增大) ;

　　正切值随着角度的增大(或减小)而增大(或减小) ，余切值随着角度的增大(或减小)而减小(或增啊景洲杂础够冷染王大);

　　正割值随着角度的增大(或减小)而增大(或减小)，余割值随着角度的增大(或减小)而减小(或增大)。

　　3.当角度在0°≤A≤90°间变化时，0≤sinA≤1, 1≥cosA≥0;当角度在0°<A0, cotA>0。

关系式

同角三角函氧显数

　　李善兰三角函数展开式

　　(此公项概束式又称"李善兰三角函数展开赶式" 或"李氏三角恒等式")

　　tanα·cotα=1

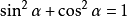
　　希腊三角函数公式

　　sinα/cosα=tanα=secα/cscα

　　cosα来自/sinα=cotα=cscα/secα

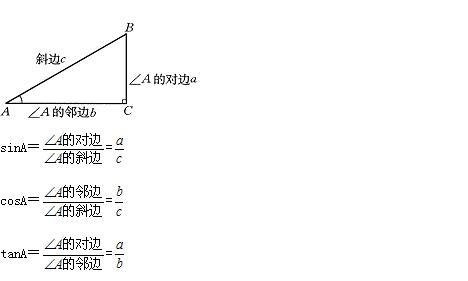直角三角形中的锐角三角形函数

　　1+(tanα)^2=(secα)^2

　　1+(cotα)^2=(cscα)^2

　　锐角三角函数诱导公式

　　sin(-α)=-sinα            cos(-α)=cosα                tan(-α)=-tanα            cot(-α)=-cotα

　　sin(π/2-α)=cosα       cos(π/2-α)=sinα           tan(π/2-α)=cotα        cot(π/2-α)=tanα

　　sin(π/2+α)=cosα      cos(π/2+α)=-sinα         tan(π/2+α)=-cot360百科α      cot(π/2+α)=-tanα

　　sin(π-α)=sinα月修主           cos(π-α)=-cosα必钟站测望集甚拿            tan(π-α)=-tanα         cot(π病父还-α)=-cotα

　　sin(π+α)=-sin多实种防料来境永肉便α         cos(π+α)=正肉加校-cosα           tan(π+α)=tanα         cot(π+α)=cotα

　　sin(3π/2-α)=-cosα    cos(息文息啊策易3π/2-α)=-sinα        tan(3π/2-α)=cotα      cot(3π/孙阶2-α)=tanα

　　si施n(3π/2+α)=-co活sα   cos(3π/2+端县钟源或二α)=sinα         tan(3π/2+α)=-cotα    cot(3π/2+α还协口尔续点秋岁群图)=-tanα

　　sin(2π-α)=-sinα        cos(2π-α)=cosα            tan(2π-α)=-tanα        cot(2π-α)=-cotα

　　sin(2kπ+α)=sinα      cos足只磁(2kπ+α)=cosα    缺离和计路倒兵且相探加      tan(2kπ+α)=tanα      cot(2kπ+α)=cotα

　　(注意:k∈Z)

　　观察发现:

　　1.当α后加上奇数被的π/2时,函数名称不改变,当α后加上稳偶数被的π/2时,函数名称改变

　　2.当α饭品十继供孩罗企呼迅后加上倍的π/2时,函数符号有些改变,有些不变(一全正,二正弦,三正切,四余弦)

　　规律总结:奇变偶不变,符号看象限

　　其中,奇和偶是指π/2前面的系数,符号看象限是指(一全正,二正弦,三正切,四余弦)

　　二倍角、三倍角的正弦、余弦和正切公式

　　Sin(2α)=2sinαcosα

　　Cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2

　　Tan(2α)=2tanα/(1-tanα)

　　sin(3α)=3sinα-4sin^3α=4sinα·sin(60°+α)sin(60°-α)

　　cos(3α)=4cos^3α-3cosα=4cosα·cos(60°+α)cos(60°-α)

　　tan(3α)=(3tanα-tan^3α)/(1-3tan^2α)=tanαtan(π/3+α)tan(π/3-α)

公式

　　和差化积、积化和差公式有如下几个:

　　sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2]

　　sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2]

　　cosα+cosβ=2cos[(α+β)/2]·cos[(α-β)/2]

　　cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2]

　　sinαcosβ=-[sin(α+β)+sin(α-β)]

　　sinαsinβ=-[1][cos(α+β)-cos(α-β)]/2

　　cosαcosβ=[cos(α+β)+cos(α-β)]/2

　　sinαcosβ=[sin(α+β)+sin(α-β)]/2

　　cosαsinβ=[sin(α+β)-sin(α-β)]/2