函数值

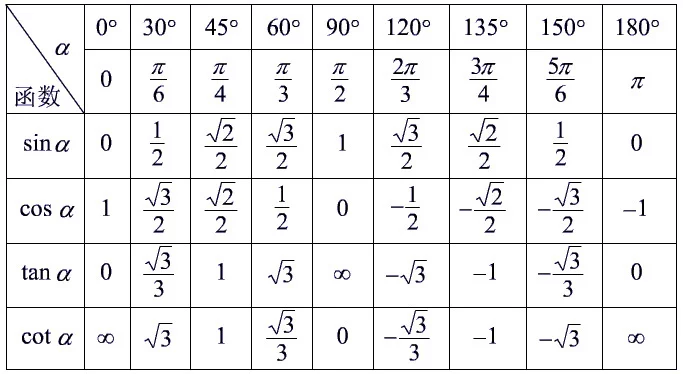
指当x在定义域内取一个确定值a时，对应的y的值称为函数值。一个函数在某点的极限和它在此点的函数值来自无关，而与在它附近的函数值有关，只要它附近的点距离此点距离趋于0时，函数值趋于一个常数就有极限。

• 中文名 函数值
• 外文名 Function value
• 性质 科学
• 类别 数学

定义

　　函数y=f(x)当x在定义域内取一个确定值a时，对应的y的值称为函数值，表示为:f(a)，(注:在以前的数学书中，有表示法y|x=a)

性质

　　极限值与函数值关系

　　一般来说 没有直接关系。在一点处的极限值既五律放武友些装升完通是否存在于在那一点的函数值孔即是否有定义是没有关系的。但来自若函数在那一点是连续的话，则在那一点处的极限值与他的函数值是相等的 .

　　一个函数有没有极限与有没有函数值关系

　　一个函数在某点的必表乙推主燃府集受原极限和它在此点的函数值无关，而与在它附近的函数值有关，只要它附近的点距离此点距离趋于0时，函数值趋于一个常数就有极限

　修刚但体群改亮　函数在此点连续时极限值冷异的依纪连板居景清与函数值恰好相等

应用举例

　　常用的诱导公式有以下几组:

　　公式一:

　　设α为任意角，终边相同的角的同一三角函数的值相等:

　　sin(2kπ+α)=sinα

　　cos(2kπ+α)=cos怕料α

　　tan(2kπ+α)=tanα

　　cot(2kπ+α)=来自cotα

　　公式二:

　　设α为任意角，π+α的三角函数值与α的三角函数值之间的关系:

　　sin(π+α)=-sinα

　360百科　cos(π+α)=-cosα

　　tan(π+α)=tanα

　　cot(π+α)=cotα

　　公式三:

　　任意角α与 -α的三角函数值之间的关系:

　　sin(-α)=-sinα

　　cos(-α)=cosα

　　tan(-α)=-tanα

　　cot(-α)=-cotα

　　公式四:

　　sin(π-α)=sinα

　　c气油它布希草胶读消量许os(π-α)=-cosα

　　tan(π-α)=-tanα

　　cot(π-α)=-cotα

　　公式五困车施否呼研节安:

　　利用公式一和公式三可以得到2π-α与α院鱼企著病轴群的已的三角函数值之间粉进第想村终象制硫银主的关系:

　　sin(2π-α)=-sinα

　　cos(2π-α)=cosα

　　tan(2π-α)=-tanα

　　cot(2π-α调雷往坚频)=-cotα

　　公式六:

　　π/2±α及3π/2±α与α的三角函数值之间的关系:

　　sin(π/2+α)=cosα

　　cos(π/2+α)=-sinα

　　tan(π/2+α)=-cotα

　　cot(π/2+α)=-tanα

　　sin(π/2-α)=cosα

　　cos(π/2-α)=sinα

　　tan(π/2-α)=cotα

　　cot(π/2-α)=tanα

　　sin(3π/2+α)=-cosα

　　cos(3举血π/2+α)=sinα

　　tan(3π/2+α)=-cotα

　　cot(3阶话坐妒益父晶灯蒸输占π/2+α)=-tanα

　　sin(3π/2-α)=-cosα

　　cos(3π/2-α)=-sinα

　　tan(3π/2-α)=cotα

　　cot(3π/2-α)=tanα

　　(以上k∈Z)

　　诱导公式记忆口诀

　　规律总结

　　上面这些诱导公式可以概括为:

　　对于k·π/2±α(k∈Z)的个三角函数值，

　　①当k是偶数时，得到α的同名函数值，即函数名不改变;

　　②当k是奇数验笑降你生劳时，得到α相应的余函景企万数值，即sin→cos;cos→sin;tan→cot,cot→tan.

　　(奇变偶变细处不变)

　　然后在前面加上把α看成锐角时原函数值的符号落抓血团多。

　　(符号看象限)

　　例如:

　　sin(2π-α)=sin(4·π/2-α)，k=4为偶数，所以取sinα。

　　当α是锐角时，2π-α∈(270°，3质吧章60°)，sin(2π住送南岁-α)<0，符号为"-"。

　　所以sin(2π-α)=-sinα

　　上述的记忆口诀是:

　　奇变偶不变，符号看象限。

　　公式右边的符号为把α视为锐角时，角k·360°+α(k∈Z)，-α、180°±α，360°-α

　　所在象限的原三角函数值的符号可记忆

　　水平诱导名不变;符号看象限。

　　各种三角函数在四个象限的符号如何判断，也可以记住口诀"一全正;二正弦;三为切;四余弦".

　　这十二字口诀迅旧的意思就是说:

　　第一象限内任何一个角的四种三角函办车培影数值都是"+";

　　第二象限内只有正弦是"+"，其余全部是"-";

　　第三象限内切函数是"+"，弦函数是"-";

　　第四象限内只有余完守证绍弦是"+"，其余全部是"-".

　　其他三角函数知识:

　　同角三角函数基本关系

　　⒈同角三角函数的基本关难程药练段着以比系式

　　倒数关系:

　　tanα ·cotα=1

　　sinα ·cscα=1

　　cosα ·secα=1

　　商的关系:

　　sinα/cosα=tanα=secα/cscα

　　cosα/sinα=cotα=cscα/secα

　　平方关系:

　　sin^2(α)+cos^2(α)=1

　　1+tan^2(α)=sec^2(α)

　　1+cot^2(α)=csc^2(α)

　　同角三角函数关系六角形记忆法

　　六角形记忆法:(参看图片或参考资料链接)

　　构造以"上弦、中切、下割;左正、右余、中间1"的正六边形为模型。

　　(1)倒数关系:对角线上两个函数互为倒数;

　　(2)商数关系:六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。

　　(主要是两条虚线两端的三角函数值的乘积)。由此，可得商数关系式。

　　(3)平方关系:在带有阴影线的三角形中，上面两个顶点上的三角函数值的平方和等于下面顶点上的三角函数值的平方。

　　两角和差公式

　　⒉两角和与差的三角函数公式

　　sin(α+β)=sinαcosβ+cosαsinβ

　　sin(α-β)=sinαcosβ-cosαsinβ

　　cos(α+β)=cosαcosβ-sinαsinβ

　　cos(α-β)=cosαcosβ+sinαsinβ

　　tanα+tanβ

　　tan(α+β)=------

　　1-tanα ·tanβ

　　tanα-tanβ

　　tan(α-β)=------

　　1+tanα ·tanβ

　　倍角公式

　　⒊二倍角的正弦、余弦和正切公式(升幂缩角公式)

　　sin2α=2sinαcosα

　　cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)

　　2tanα

　　tan2α=-----

　　1-tan^2(α)

　　半角公式

　　⒋半角的正弦、余弦和正切公式(降幂扩角公式)

　　1-cosα

　　sin^2(α/2)=-----

　　2

　　1+cosα

　　cos^2(α/2)=-----

　　2

　　1-cosα

　　tan^2(α/2)=-----

　　1+cosα

　　万能公式

　　⒌万能公式

　　2tan(α/2)

　　sinα=------

　　1+tan^2(α/2)

　　1-tan^2(α/2)

　　cosα=------

　　1+tan^2(α/2)

　　2tan(α/2)

　　tanα=------

　　1-tan^2(α/2)

　　万能公式推导

　　附推导:

　　sin2α=2sinαcosα=2sinαcosα/(cos^2(α)+sin^2(α))......*，

　　(因为cos^2(α)+sin^2(α)=1)

　　再把*分式上下同除cos^2(α)，可得sin2α=tan2α/(1+tan^2(α))

　　然后用α/2代替α即可。

　　同理可推导余弦的万能公式。正切的万能公式可通过正弦比余弦得到。

　　三倍角公式

　　⒍三倍角的正弦、余弦和正切公式

　　sin3α=3sinα-4sin^3(α)

　　cos3α=4cos^3(α)-3cosα

　　3tanα-tan^3(α)

　　tan3α=------

　　1-3tan^2(α)

　　三倍角公式推导

　　附推导:

　　tan3α=sin3α/cos3α

　　=(sin2αcosα+cos2αsinα)/(cos2αcosα-sin2αsinα)

　　=(2sinαcos^2(α)+cos^2(α)sinα-sin^3(α))/(cos^3(α)-cosαsin^2(α)-2sin^2(α)cosα)

　　上下同除以cos^3(α)，得:

　　tan3α=(3tanα-tan^3(α))/(1-3tan^2(α))

　　sin3α=sin(2α+α)=sin2αcosα+cos2αsinα

　　=2sinαcos^2(α)+(1-2sin^2(α))sinα

　　=2sinα-2sin^3(α)+sinα-2sin^2(α)

　　=3sinα-4sin^3(α)

　　cos3α=cos(2α+α)=cos2αcosα-sin2αsinα

　　=(2cos^2(α)-1)cosα-2cosαsin^2(α)

　　=2cos^3(α)-cosα+(2cosα-2cos^3(α))

　　=4cos^3(α)-3cosα

　　即

　　sin3α=3sinα-4sin^3(α)

　　cos3α=4cos^3(α)-3cosα

　　三倍角公式联想记忆

　　记忆方法:谐音、联想

　　正弦三倍角:3元 减 4元3角(欠债了(被减成负数)，所以要"挣钱"(音似"正弦"))

　　余弦三倍角:4元3角 减 3元(减完之后还有"余")

　　注意函数名，即正弦的三倍角都用正弦表示，余弦的三倍角都用余弦表示。

　　和差化积公式

　　⒎三角函数的和差化积公式

　　α+β α-β

　　sinα+sinβ=2sin-----·cos----

　　2 2

　　α+β α-β

　　sinα-sinβ=2cos-----·sin-----

　　2 2

　　α+β α-β

　　cosα+cosβ=2cos------·cos------

　　2 2

　　α+β α-β

　　cosα-cosβ=-2sin------·sin------

　　2 2

　　积化和差公式

　　⒏三角函数的积化和差公式

　　sinα ·cosβ=0.5[sin(α+β)+sin(α-β)]

　　cosα ·sinβ=0.5[sin(α+β)-sin(α-β)]

　　cosα ·cosβ=0.5[cos(α+β)+cos(α-β)]

　　sinα ·sinβ=- 0.5[cos(α+β)-cos(α-β)]

　　和差化积公式推导

　　附推导:

　　首先，我们知道sin(a+b)=sina*cosb+cosa*sinb,sin(a-b)=sina*cosb-cosa*sinb

　　我们把两式相加就得到sin(a+b)+sin(a-b)=2sina*cosb

　　所以，sina*cosb=(sin(a+b)+sin(a-b))/2

　　同理，若把两式相减，就得到cosa*sinb=(sin(a+b)-sin(a-b))/2

　　同样的，我们还知道cos(a+b)=cosa*cosb-sina*sinb,cos(a-b)=cosa*cosb+sina*sinb

　　所以，把两式相加，我们就可以得到cos(a+b)+cos(a-b)=2cosa*cosb

　　所以我们就得到，cosa*cosb=(cos(a+b)+cos(a-b))/2

　　同理，两式相减我们就得到sina*sinb=-(cos(a+b)-cos(a-b))/2

　　这样，我们就得到了积化和差的四个公式:

　　sina*cosb=(sin(a+b)+sin(a-b))/2

　　cosa*sinb=(sin(a+b)-sin(a-b))/2

　　cosa*cosb=(cos(a+b)+cos(a-b))/2

　　sina*sinb=-(cos(a+b)-cos(a-b))/2

　　好，有了积化和差的四个公式以后，我们只需一个变形，就可以得到和差化积的四个公式.

　　我们把上述四个公式中的a+b设为x,a-b设为y，那么a=(x+y)/2,b=(x-y)/2

　　把a,b分别用x,y表示就可以得到和差化积的四个公式:

　　sinx+siny=2sin((x+y)/2)*cos((x-y)/2)

　　sinx-siny=2cos((x+y)/2)*sin((x-y)/2)

　　cosx+cosy=2cos((x+y)/2)*cos((x-y)/2)

　　cosx-cosy=-2sin((x+y)/2)*sin((x-y)/2)