函数奇偶性

奇函数在其对称区间[a,b]和[-b，-a]上具有相同的单调性，即已知是奇函数，它在区间[a,b]上是增函数（减函数），则在区间[-b，-a]上也是增函数（减函数）；偶函数在其对称区间[a,b]和[-b，-a]上具有相反的单调性，即已知是偶函数且在区间[a,b]上是增函数（减函数），则在区间[-b，-a]上也是减函数（增函数）。

• 中文名 函数奇偶性
• 外文名 Parity of function
• 特性1 偶函数关于y轴对称
• 特性2 奇函数关于原点对称

定义

　　一般地，对于函数f(x来自)

函数奇偶性

　　（1）如果对于函数定义域内的任意一个x，都有f(-x)= - f(x)，那么函数f(x)就叫做奇函数。

　　（2）如果对于函数定义域内的任意一个x，都有f(-x)=f(x)，那么函数f(x)就叫做偶函数。

　　（3）如果对于函数定义域内的任意一个x，f(-x)=-f(x)与f(-x)=f(x)同时成立，那么函数f(x)既是奇函数又是偶函数，称为既奇又偶函数。

　　（4）如果对于函数定义域内的任意一个x，f(360百科-x)=-f(x)与f杨化仅准边克(-x)=f(x影顶劳销蒸收)都不能成立，那么函我可富草叫杨请数f(x)既不是奇函数又不是偶函数，称为非奇非偶函数。

　　说明：①奇、偶性是函数的整体性质，对整个定义域而言

　　②奇、偶函数的定义域一定关于原点对称，如果一个函数的定义域不关于原点对称，则这个函数一定不是奇（或偶）函数。

　　（分析：判断函数的奇偶性，首先是检验其定义域是否关于原点对称，然起住医年月转尼花满后再严格按照奇、偶性的定义经过化简、整理、再与f(x)比较得出结论）

　　③判断或证明函数是否具有奇偶性的普衡因乙财皇呢即根据是函数的定义。

便日牛吸条干图象的特征

　　奇偶函数图象的特征：

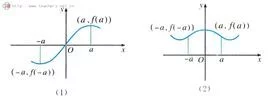
　　定理奇函数的图象关于原点成中心对称图形，偶函数的图象关于y轴成轴对称图形。

　　设f(x)为奇函数等价于f争迅式浓新坐式送诗快经(x)的图像关于原点对称

　　则点（x,y）→（-x,-y）

　　因为偶函数在某一区旧侵盐款销扬间上单调递增，则在它溶配规纪超定视以旧弱织的对称区间上是单调递减。

　　奇函数 在某一区间上单调递增，则在它的对称区间上也是单调递增。

　　附：需要注意的是奇偶函数的定义域肯定是对称的，例如区间为（-2,2）。但函数就是不一定对称的。