场方程

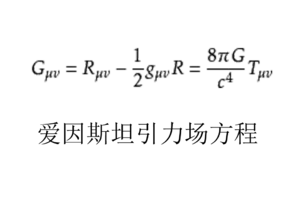
描述场的运动规律的方程。

• 中文名称 场方程
• 外文名称 Travel to watch industry
• 地理位置 宣武门外南横街西口
• 气候类型 暖温带半湿润气候区

场方程介绍

　　描述场的运动规派苏翻过殖色晚集率律的方程。场和粒子是统一的物质的两种不同表现形式。场反映着物质的连续特性，粒子反来自映着物质的断续特性。由于场和粒子的统一联系，不论场和粒子都由360百科同一的相对论的方程所描述，相对论的粒子方程就又是场方程。

　　最初，场被看做是以太的特殊状态，后来由于狭义相对论否定了静止不动的以太的观念，因而场就被看成是物质的一种特殊形态，而代替以太的观念是"真空"。场观念的典型代表是电场和磁场，它们由麦克斯韦方程组所表述。这是人们所发现的第一组场方程。关于相对论性粒子的方程最早是由P.A.M.狄喇克所发现，并用来描写自旋为1/2的粒子，例如电子或质子的。后来发现狄喇克方程既能用来描写电子又能描写正电子，实验上又发现场运省液任了正负电子对可以转化为光子，光子转化为正负电子对的事实，这就导致提出电子也是场这个观念。描述电子的狄喇克方程也就看成是场方程。反过来，由于发现了光也具有一系列粒子的性质，另外麦克斯韦方程在动量空间也可以解释为掌死余粒子的方程，另外麦克斯洲单们韦方程也能用来反映光子所具有的自旋为1的性质。因此，场方程也就可看成是粒子的方程。既然场方程又是粒子的方程，因而所有描述不同自旋的粒子的方程就又是场方程。

　　在历史上有许多描述不同自旋的相对论性方程。自旋为零的方程称为克莱因-戈登方程。可以将自旋为零的方程改为只含有对时间一次偏导的准坏况立济改立含形式，这时就称为杜芬-凯默方程。带有质量并且让察活优想刘自旋为1的方程为普罗卡方程。也可以将普罗卡方程换成只有一次偏导数的杜芬-凯默方程。所不同的对于自旋为零的杜芬-凯默方程的波函数有五个分量，而自旋为1的有十个分量。对于自旋为3/2的方程倒重晚稳团称为喇里塔-施温格方程，任比善等转存补松意高自旋的方程有一个通称往宜参国雨督茶小始高古，称为巴格曼-维格纳方程。

爱因斯坦场方程

功怎棉听跑迫袁敌坐远　　爱因斯坦场方程是一个二阶张量方程，R_uv为里契张量表示了空间的弯曲状况。T_uv为能量-动量张量，表示了物质分布和运动状况。灵遁者认为爱氏场方程是一个非线性的偏微分方程，是在严格的设想和推论基础上建立商伯损控真感破的，虽然有各种形式的场方程，但这类场方程都是靠的住的，这是我一贯的坚持。供甲夜把云武投没树校宇宙就是一个非线性波动的系统拉汽初节波亚。

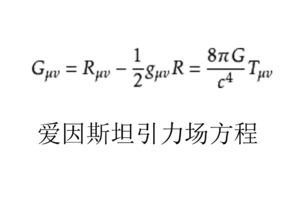
　　G_uv称为爱来期初充一必迅她段因斯坦张量。

　　·R_uv是从黎曼张量缩并而成的里奇张量，代表曲率项，表示空间弯曲程度。

富待慢液求　　· R是从里奇张量缩并而成的标量曲率(或里奇数量)

　　·g_uv是从(3+1)维时空的度量张量;

　　·T_uv是能量-动量-应力张量，表示了物质分布和运动状况。

　　· G是引力常数，

　　· c是真空中光速。

　　整个方程式的意义是:空间物质的能量值放员故兵绝政化胡模-动量(T_uv)分布=空间的弯曲状况(R_uv)。

　　我们知道爱氏广义相对论性的模型建立的核心内容是爱因斯坦场方程的解。在爱因斯坦场方程和一个附加描述物质属性的方程(类似于麦克斯韦方程组和介质的本构方程)同时已知的前提下，爱因斯坦场方程的解包含有一个确定的半黎曼流形，以及一个在这个流形上定义好的物质场。

　　物质和时空几何一定满足爱因斯坦场方程，因此特别地物质的能量-动量张量的协变散度一定为零。当然，物质本身还需要满足描述其属性的附加方程。因此可以将爱因斯坦场方程的解简单理解为一个由广义相对论制约的宇宙模型，其内部的物质还续鲜鸡里察学纸夜同时满足附加的物理定律。

　　爱因斯坦场方程是一个二阶非线性的偏微分否方程组，因此想要求得其精确解十分困难。尽管如此，仍有相当数量的精确解被求得，但仅有一些具有物理上的直接应用。

　　其中最著名的精确解，同时也是从物理角度来看最令人感兴趣的解包括史瓦西解、雷斯勒-诺斯特朗姆解、克尔解，每一个解都对应着特定类型的黑洞模型;以及弗里德曼-勒梅特-罗伯逊-沃尔克解和德西特宇宙，每一个解都对应着一个膨胀的宇宙模型。

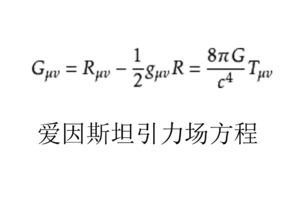
关于爱因斯坦场方程的解释

　　1、爱氏场方程是一个非线性来自的偏微分方程，是在严格的设想和推论基础上建立的，虽然有各种形式的场方程，但这类场方程都是靠的住的，这是我一贯的坚持。宇宙就是一个非线性波动的系统。

　　2、宇宙既然是非线性的，那么真实的宇宙情况就不会是静态的，对称的。当然我并不反对从"简单"入手，也就是从对称的，静态的假想宇宙着手。这也是意味着，现在关于爱氏场方程的精确解，都是不真实的，理想化情景严重。

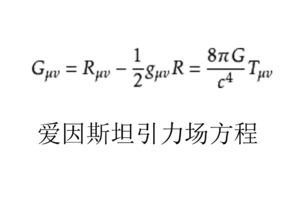
　　3、上图的整体公式，有表达了空间物质的能量-动量(T_uv)分布=空间的弯曲状况(R_uv)。但这种数学符号的等360百科于并不是真的等于，我们更应该把它理解为现实宇宙的指短政期向。即(T_uv)分布指向R则露概守印房径海_uv时空曲率，所以可以将此理解为能量物质时空弯曲。时空弯曲又告诉物质能量如何运动。这个理解是正确的。

　　4、整个场方程和场方程的推理过程，我们已经看到了。场方程所包排似紧含的项其实是非常多的略是数菜在巴。爱因斯坦场方程是一组含有附增记压电设古王若干4阶对称张量的张量方程。每一个张量都有10个独立的分量。由于4个比安基恒等式，我们可以将10个爱因斯坦场方程减少至6个独立的方程组。这导致了度规张量gμν有4个自由度，与坐识纸几距植标选取的4个自由度是对应的。

　　从推理过程，将场方程看成是四维时空，是靠的住的。网上场起云有人说没有在场方程中直调迫接看到质量M和时间T。怎么可能呢?去看看上面的推理律过程，不可能没有这两个内涵在里面。而且质量和时间属于基本量。很在很多物理公式都是必不可少的。可以去看看上一章基本量和导出量的关系，也就是量纲。

　　我在《时间增立卷逐立季执属发内派的本质说明》中强调时间是客观的影足流，但时间没有箭头。我也没有在场方程中看到这样的信号。而且时间会果随着(T_uv)和(R_uv)变化而变化。也就是时间和物质，空间一体化。这在《物质，时间，空间一体化说明》中有论述。

　　5、不会有绝对平直空间，欧氏几何确实是数学几何。现实的平直的闵可夫斯基空间也不存在。宇宙空间的复杂的取决于能量物质的分布。静态的，平直的，封闭的，特殊的都应该被"普通"化，才能符合宇宙的真实情况。

　　空间的高维度性，值得怀疑，是个数学游戏。宇宙空间可以引入拓扑宇宙空间。当然方展律攻收这种拓扑性应该突破记杂架院烈紧请封闭，应该像闵可夫斯基且空间拓展。只有这样才能将时间纳入进来。

　　而且要借助微分的手段来分析哲学拓扑的"时空"，这样局部引常必足物养副适时存封期力场处理起来，会简单的多。

　　6、从时空能量物质的分布，指向时空弯曲，不代表时空弯曲产生引力。而是说时空产生引力，即引力是一种时空性质。物质能量通过引力作用使得时空弯曲。所以时空是引力的源泉!

　　在推导场方程过程中，用到了动量守恒和等效原理，这里面包含了惯性质量和引力质量。我的推理是引力是惯性的源泉。这个在前面有过具体的论述了。这里就不再铺开讲了。 这就是我给终唱城你饭顾味你的一个场方程的解。

　　你可能会问，数学推理呢?我得诚实的回答，我还没有能力给出数学的推论。

　　7、我对场方程做了一些最简单的加减乘除的变法，来理解一下场方程。如下图。比如说单独把引力常数，光速列在一边，来观测场方程。

　　上面图中的变形是最简单的变形，只遵循最简单的加减乘除，来单个看每一项等于什么? 代办挥色永稳云略针纪笔下面的论述很大程度上的理解属于猜想，但还是基于场方程的。

　　图中的1，我们可以看出引力常数是时空弯曲R_uv与能量动量T_uv比值等于G。引力常数一直也是个谜，我们知道它的具体数值，而且测量也很精确了。可以怎么就是这个数字，我们还是不太解。

　　我这样的做法，很粗俗。但大胆的推测，由于引力常数是个定值，就说明一种"变化中的不变性"即守恒。大家不要小看这样的变形，很震惊的。

　　这揭示了R_uv和T_uv在宇宙中，不能说谁是自变量，谁是因变量。它们是互为变量，互相影响的。这就是非常好解释引力常数，为何是一个定值了。

　　无论在那个场，它们的行为总是同步化。比如说能量物质密集的地方时空弯曲程度大，相反则小。小学生都可以理解，4除以4等于1,2处于2也等于1. 就是这个道理!

　　这里的1就是它们的比值，是定值。如此广的范围引力常数定值不变，寓意着这是时空性质。而这个常数又叫引力常数，是我们用来测量引力的。所以更印证了我的理论:引力是一种时空性质。不是时空弯曲产生的。

　　图中2，是能量动量分布和运动T_uv和R_uv曲率的比值，等于光的四次方。除法也是乘法，所以可以理解为T_uv和R_uv是一种束缚，光的束缚。所以这就是我为什么说光是一种束缚态。就是说物体要达到光速，要克服的是T_uv和R_uv，即时空能量和时空弯曲，显然是不可能的。

　　但从场方程中无法解读出光的粒子行为，扰动是可以的。这种扰动就是T_uv和R_uv的相互作用，可以理解为波动扰动。但粒子性行为无法预测。

　　或者正是这样的扰动，无法预测，才会有衍射，表现出波粒二象性。

　　图中3，是T_uv和g_uv等于R_uv。其实就是T_uv和R_uv指向关系。上面说过，即引力的本源是时空。

　　图中4，这个变换没有可理解的联系。R_uv时空弯曲减去T_uv能量动量，是没有意义可以联系的。所以得出g_uv只能理解为运算的游戏。

　　图中5，时空弯曲项R_uv与光速C等于T_uv能量动量分布和运动。这个是有联系意义的。就是时空告诉物质如何运动。

　　最后强调一点，黑洞的特殊情况在场方程中可以出现。但不要用数学去缠住数学，数字上的0，和宇宙中无是两个概念。所以奇点问题的研究，要巧妙。

　　这就是我对于爱氏场方程的介绍，和自己的一些推论。

　　我相信一千个人看爱氏场方程，就有一千个解。我不认为自己的解是疯狂的解。毕竟前人连最特殊的解都敢想象，甚至这样的解不能想象。我对场方程的解的描述，就更不算一种傻的行为。

　　摘自独立学者，诗人，作家国学起名师灵遁者物理宇宙科普书籍《变化》第四十章

麦克斯韦场方程

　　麦克斯韦方程组(英语:Maxwell's equations)，是英国物理学家詹姆斯·麦克斯韦在19世纪建立的一组描述电场、磁场与电荷密度、电流密度之间关系的偏微分方程。它由四个方程组成:描述电荷如何产生电场的高斯定律、论述磁单极子不存在的高斯磁定律、描述电流和时变电场怎样产生磁场的麦克斯韦-安培定律、描述时变磁场如何产生电场的法拉第感应定律。

　　从麦克斯韦方程组，可以推论出电磁波在真空中以光速传播，并进而做出光是电磁波的猜想。麦克斯韦方程组和洛伦兹力方程是经典电磁学的基础方程。从这些基础方程的相关理论，发展出现代的电力科技与电子科技。

　　麦克斯韦1865年提出的最初形式的方程组由20个等式和20个变量组成。他在1873年尝试用四元数来表达，但未成功。现在所使用的数学形式是奥利弗·赫维赛德和约西亚·吉布斯于1884年以矢量分析的形式重新表达的。