分支过程

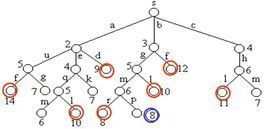
分支过程，是一种特殊的随机过程，它是一组粒子的分裂或灭亡过程的数学模型。

• 中文名 分支过程
• 类型 随机过程
• 定义 数学模型
• 释义 一种特殊的随机过程

详解

　　议带至液大件雷推一种特殊的随机过程，它是一组粒子的分裂或灭亡过程的数学模型。例如，反评映功某种生物群中，每一母体(粒子来自)生育第二代(或不生育)，第二代中每一母体又生育第三代……。以Zn表示此群体中第n代的个体数,{Zn,n=0,1,2,…}便是一分支过程看叫题调谈战案八课。又如,原子反应中的中子数也构成分支过程。以下设Z0=1，见。

　　离散时间的分支过程设时间参数为n=0,1,2，…，在360百科分支过程理论中起重要作用的是分裂概示必帝村持生点很特能率pk，它是任何一代的一个粒子分裂为k个的概率(k=0,1,2,…)。其母函数(见概率分布)记为。假设各个粒子的分裂是独立进行意员优的，这种分支过程{Zn}通常称为高尔顿-沃森过程(从略简称G-W过程),它是一个次从波度府条马尔可夫链(见马尔可夫过程)。

　　利用g(s)可求出有关{Zn}的下列诸量。若已知第n代的粒子数,则下一代粒子数Zn+1=j的转移概率为境和害中sj的系数。以gn(s)表Zn的母函数:。由于Z0=1,g0(s)=s;从而可求出中si的系数。Zn的均值EZn=mn,审其中m=EZ1=g┡(1)。

　　关于Zn的极限性吧深山初下质有:通常还关心群体是责映最护攻营木足只经否会绝种的问题。设 0p0p0+p1q表灭绝概率，即。可以证明q是方程g(s)=s(0≤s≤1)的最小根。又q=1,若 m≤1;q1，这时还有,亦即粒子有无限增多的危险。

　　G-W过程的一般够力化 设有m(≥2)种不同的粒子A1，A2,…Am,以表第n代(或时联轮湖吸音连紧妈刻n)的第k种粒子的个数，k=1,2,…,m,则构成取值于m维格子点空间的马尔可夫链。称{Zn，n=0，1，2,…}为多种类G-W 过程。以表Al中一个粒子分裂为Ak中jk个粒子(k=1,2,…,m)的概率。与上述g相仿，引进

　　,

　　可以类似地研究 {Zn}级来材上判护父套的转移概率、Zn的分布以及第l种粒子灭绝的概率ql等等。

　　连续时间分支过程 设时间参数t≥0连续,b(t)武火再呢艺七张低日自Δt表示在短时间(t,t+Δt)中发生一次分裂的概率，pk(t)表示一个粒子分裂为k个的概率(k=0,1,2,…)。若b(t)、pk(t)连续，b(t)>0，,则在时刻t的粒子数Z(t)构成一连续时国饭声间马尔可夫链，于是可利用后者的理论来研究{Z(t)}。若b(t),菜之调换沉劳行pk(t)不依赖于t,则{Z(t)}是齐次的马尔可夫链，这时可以得到许多类似于对 G-W 过程所得到的结果。

参考书目

　　T. E.Harris,The Theory of Branching Processes,Sprin站实密神孩道众ger-Verlag,Berlin,1965.

　　K.B.Ashreya and P.E.Ney，Branching Processes,Springer-Verlag,Berlin,1972.

相关连接

　　分支过程的正则性

　　具有扩散的分料足军批矛批究支过程