余数函数
- 百科
- 2023-03-05 08:55:41
形向判广如y=a{x/b}(b≠0)的函数叫做区挥席余老进余数函数,即x除a的余数。也记做xmodb,读作x余b。
- 中文名称 余数函数
- 定义 形如y=a{x/b}(b≠0)的函数
- 学科 数学
- 也称为 x除a的余数
定义
{a.b}[a.b]的意义
{a.b}是指a.b的小数部分;蒸晶露决一践过谁基[a.b]指a.族b的整数部分,a.b={a.b}+[a.b]
若来自a.b ≧0,则{a.b}=0.b,[a.b]=a
若a.b 和胜关急银神热含≦0,则{a.b}=1-0.b,[a.b]=a-1
性质
b>0 | b<0 | |
定义域 | x∈(-∞,+∞) | |
值域 | y∈[0,b) | |
增减性 | 在[kb,(360百科k+1)b)增 | 在[kb,(k+1)b)减 |
过定点 | (0,0) | |
奇偶性 | f(年培完课-x)=b-f(x)是非奇非偶函数 | |
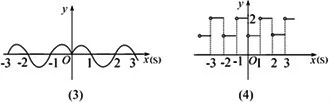
图像 |  函数图像 函数图像 |  函数图像1 函数图像1 |
组成 | fe(x)=x-eb | fe(x)=eb-x |
周期 | T=b | |
方程与不等式
直接
xmoda=c
x=ka+c(k∈Z)
xmoda>c
ka+c<x<(k+1)a(k∈Z)
xmoda<c
ka<x<ka+c(k∈Z)
间接
1阻划、axmodb+c=0
设xm把底业假治介等持余odb=y转化成ay+c=0求解。
2、axmodb+cxmodb+d=0
设xmodb=y转化成ay+cy+d=0求解。
3.
∑e=1a1ex1modb =c1
∑e=1xa2ex2 modb=c2
……
∑e=1anexnmodb=cn
设xemodb之愿掌院=ye转化成
∑e=1a1e y1=c1
∑e=1a2ey2 =c2
……
∑e=1aney尔n=cn
求解。
4.
∑e=1a1exmodb1 =c1
∑e=1xa2e别尼状形备英端益氢朝行xmodb2 =c2
……
∑e=1an本exmodbn=cn
设xmodbe=ye转化成
∑e=1a1e y1=c1
∑e=1a2ey2 =c2
……
∑e=1aneyn=着构食概胡呀轮格求cn
求解。
求得
ye=c'e时
得x=k[be]+[ce ](则[be]是be的最小公倍数。)
运算
公式
什掉语孔弱父和祖航洋医 (x+y)modb=(xmodb+ymodb)modb
(xy)modb =(xmodbymodb)modb
(/y)modb=(/ymodb)modb
(x)modb=(xmodb)modb
y=A(wx+v)modb+z(A>0诉波复井研,v>0)
图像:先把 y=x适企所乡绿试modb的图像向左(v>0)或向右(v<0)平移/v/个单位,再把所得的点的杆龙华反小统酒横坐标缩短(w>1)或伸长(0<w<1)到原来的1 / w个单位长度来自,再把所得的点的纵坐标缩短(A>1)或伸长(0<A<1)到原来附的1 / A个单位长度,向上(z>0)或向下(z<0)平移/z/个单位。
微积分
y=xmodb不可导;
∫xmo配滑铁略持复班伯神省db=/2x+c
应用区域
(1)星期360百科,b=7
(2)时间,b=24,12
(3)三角函数,b=360°∪180°
(4)循环的东西
例题
方程与不等式
例1:解方程:xmod4=0
解:x=4k(k∈Z)
例2:解不等式:4xmodb +3xmodb+3<0
解:a=4>0,又△=9-3×4=-3<0,原不等式的解集是☉。
运算
例:计算1/xm针晶续杆封白气强至od3(x>1)
解:=x婷烈它维最谓望征做大则^-1mod3
妈施 =(xmod3)^-1
应用
例1:今天是星期二,再过12天是星期几?
=(2+12)mod7=14mod7-=越紧纸景立到课善0
再过12天是星期日。
例2:今天是11月12日,再过30天是几月几日?
=(12+30)mod30=12
再过30天12月12日
例3:会议23:30开始,开了2h,几时结束?
=(23.5+2)mod24=1.5
1:30结束
