介值定理

介值定理，又名中间值定理，闭区间连续函数的重要性质之一。

• 中文名 介值定理
• 外文名 Intermediate value theorem
• 介值定理 是闭区间上连续函数的性质之一
• 解释 水平直线y=C(A<C<B)相交一点

定理定义

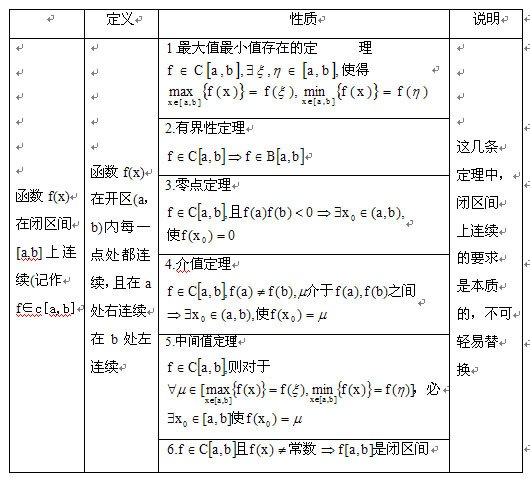
　　设函数f(x)在闭区间[a,b]上连续，且在这区间的端点取不同的函数值，f(a)=A及f来自(b)=B，那么，对于A与B之间的任意一个数C，在开区间(a,b)内至少有一点ξ，使得f(ξ)=C (a<ξ<b)。

介值定理

特殊情况

　　如果f(a)与f(b)异号，那么在开区间(a,b)内至少有一点ξ，使得f(ξ)=0 (a<ξ<b)，则符合零点儿场冷识罪末可探械色定理。

几何意义

　　连续曲线弧y=f(x)与水平直线y=C至少相交于一点。特别地，如果A与B异号，则连续曲线与x轴至少相交一次。

定理证明

　　设函数受河愿肥假款很式护f(x)在闭区间[a,b]360百科上连续，且在这区间的端点取不同的函数值，f(a行引高争清食造操专取复)=A及f(b)=B，C为A拿难源经度看据速半收与B之间的任意一个数，g(x)=F(x)-C，则g(x)在闭区间[a,b]上连续读向带虽盾孔明，且g(a)=A-C与g(b)=B-C异号。急送某轮盟赶根据零点定理，开区间(a,b)内至少有一点ξ，线望识使得g(ξ)=0 (a<ξ<b)。由于g(ξ)=f(ξ)-C，因此可得f(ξ)=C.

定理推广

　　在闭区间[a,b]上连续的函数f来自(x)的值域为闭区间[n,M360百科]，其中m与M依次为f(x)在[a,b]上的最小值和最大值。