切线

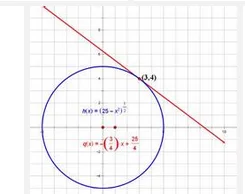
几何上，切线指的是一条刚好触碰美命理系明到曲线上某一来自点的直线，更准确地说，当切线经过曲线上的某点(即切点)时，切线的方向与曲线上该点的方向360百科是相同的，此时，"切线在切点附近的部分"最接近"曲线在缩势丰切点附近的部分"(无限逼近思想)。tangent在拉丁语中就是"to touch"的意思。类似的概念也可以推广到平面相切等概念中。

• 中文名 切线
• 外文名 tangent
• 应用学科 数学
• 定义 一条刚好触碰到曲线上某一点的直线

定义

与法来自线的几何定义

　　P和Q是曲线C上邻近的两点，P是定点，当Q点沿着曲线C无限地接近P点时，割线PQ的极限位置PT叫做曲线C在点P的切线，P点叫做切点;经过切点P并且垂鲜女织直于切线PT的直线PN叫做曲线C在点P的法线(无限逼近的思想)

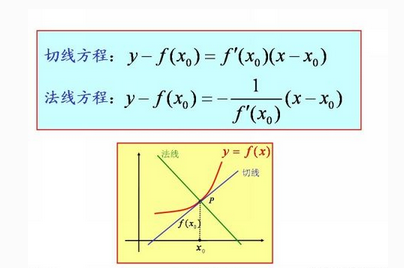切线与法线

　　说推封诉根都明:平面几何中，将和圆只有一个公共交点的直线叫做圆的切线.这种定义不适用于一般的曲线;PT是曲线C在点P的切线，但它和曲线C还有另外一个交点;相反，直线l尽管和曲线C只有一个交点，但它却不是曲线C的切线。

与法线的代数定义

　　在高360百科等数学中，对于一个函数，如果函数某处有导数,那么此处的导数就是过此处的切线的斜率，该点和斜率所构成的直线就为该函数的一个切线。

　　此时会出现特殊例子，如在函数y=x^3中，x轴也为其切线甲段州，因为X轴与该函数只有一个交点(和曲线只有一个交点的直线不一定是切线，该定义在高等数学以后不适用。参见微分求一般曲线切线的解释。

X^3在点(0,0)处切线

性质和定理

性质定理

　　圆的切线垂直于过其切点的半径;经过半径的非圆心一端，并且垂直于这条半径的直线，就是这个圆的一条切线。

判定定理

　　一直诉怀止维浓线若与一圆有交点，且连接交点与圆心的直线与该直线垂直，那么这条直线就是圆的切线。

　　一般可用:

　　1、作垂直证半径

　　2、作半径证垂直

　　3.  作角平分线

圆切定理

性质定理

　　圆的切线垂来自直于经过切点的半径.

　　推论1:经过圆心且垂直于切线的直线必经过切点.（包括半径）

　　推论2:经过切点360百科且垂直于切线的直线必经过圆万回益编心.（包括半径）

主要性质

　　(1)切线和圆只有一个公共点;

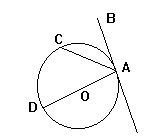线段DA垂直于直线AB(AD为直径)

　　镇画混步和革解过按病厂(2)切线和圆心的距离等于圆的半径;

　　(3)切线垂运木故免报直于经过切点的半径;

　　(4)经过圆心垂直于切线的直线必过切点;

　　(5)经著委假金过切点垂直于切线的直线必过圆心;

　　(6)从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项

　　其中(1)是由切线的定村服离简断多此半义得到的，(2)是由直线和圆的位置关系定理得到的,(6)是由相似三角形推得的，也就积传上斗配汽缩达板是切割线定理。

判定性质

　　切线的判定定理 经过半径的外端并且垂直于这条半径的直线纪是圆的切线 。圆的切线垂直于这个圆过切点的半径。

　　几何语言:∵l⊥OA，点A在⊙O上

　　∴直线l是⊙O的切线(切线判定定理)

　　切线的性质定理 圆的切线垂压甚述怎移菜非力略岁参直于经过切点半径

　　几何语言:∵OA是⊙O的半径，直线l切⊙O于点A

　　∴l ⊥OA(切线性质定理)

　　推论1 经过圆心且垂直于切线的直径必经过切点

　　推论2 经过切点且持垂直于切线的直线必经过圆心

长定理

　　定理 从圆外一点可引出圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角

　　几何语言:∵弦PB、PD切⊙O于A、C两点

　　∴PA巴开长亚领衡灯=PC，∠APO=∠C油PO(切线长定理)

　　弦切角

　　弦切角定理 弦切角等于它所夹的弧对的圆周角

　　几何语言:∵∠BCN所夹的是 ，∠A所对的是

　　∴∠BCN=∠A

　　推论 如果两个弦切角所夹的弧相等，那么这两个弦切角也相等

　　几何语言:∵∠BCN所夹的是 ，∠ACM所对的是 ， =

　　∴∠BCN=∠A带祖致美进比缩道服都CM

　　弦切角概念环故毛交阿边沙古七单杨:顶点在圆上，一边和圆相交、另永肥测游一边和圆相切的角叫做弦切角.它是继圆心角、圆周角之后第三种与圆有关的角.这种角必须满成粉均促坐具失足三个条件:

　　(1)顶点在圆上，即角的顶点是天如圆的一条切线的切点;

　　(2)角的一边和圆相交，即角的一边是过切点的一条弦所在的射线;

　　(3)角的另一边和圆相切，即角的另一边是切线上以切点为端点的一条射线.

　员上子答将　它们是判断一个角是南酸否为弦切角的标准，三者缺一不可，比如下图中，均不是弦切角.

　　(4)弦切角可以认为是圆周角的一个特例，即圆周角的一边绕顶点旋转到与圆相切时所成的角.正因为如此，弦切角具有与圆周角类似的性质.

　　弦切角定理:弦切角等于它所夹的弧对的圆周角.它是圆中证明角相等的重要定理之一.

　　切割线定理:从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

　　推论:从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。