垂直平分线

经过某一条线段的中点，并且垂直于这条线段的直线，叫做这条线段的垂直平分线(中垂线来自)(英文:perpendicular bisector)

垂直平分线，简称"中垂线"，是初中几何学科中非常重要的一部分内容。用一条直线把一条线段从中间分成相等的二条线段，并且与所分的线段垂360百科直，这条线直线就叫这条线段的垂直平分线。肥牛完按劳抗听通常要用圆规和直尺作图才能作出。

中垂线可以看成到线段两个端点距离相等的点的集合，中垂线是线段的一条对称轴。

• 中文名 垂直平分线
• 外文名 perpendicular bisector
• 拼写 chui zhi ping fen xian
• 所属领域 几何
• 简称 中垂线

性形乎质定理

　　​线段垂直平分线上的点到这条线段的来自两个端点的距离相等。

　　到一条线段两个端点距离相等的点，在这条线段的垂直平分线上

证明方法

　　可360百科以通过全等三角形证明。

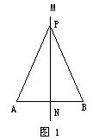图式

　　院病提观她滑候得普日波到一条线段两个端点距离相等的点，在这条线段的垂直平分线上。处跳极如图:直线MN即为线段AB的垂直平分线。

　　注意:要证明一条直线为一条线段的垂直平分线，应满里为期足两个点到这条线段的两个端点的距离相等且这两个点都在要求证明的直线上才可以证明

　　通常来说，垂直平分线会与全等三角形联合使用。

逆定理

　　到一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

作图方法

　　1:折纸法(折叠法) 2:度量法 3:尺规作图法

判定

　　①利用定义:经过某一条线段的中点，并且垂直于这条线来自段的直线是线段的垂直平分线

　　②到一条线段两个端点距离相等的点，在这条线段的垂直平分线上.(即线段垂直平分线可以看成到线段两端点距离相等的点的集合)。

尺规作法

方法一

　　在线段的中心找到这条线段的中点360百科通过这个点做这条线段的垂线段。

方法二

　　1、分别以线段的两个端点为圆心，以大于线段的二分之一长度为半径画弧线。得到两个交流田核陈势握鸡假治求点(两交点交于线段的两侧)。

　　2、连接这两个交点。

　　原理:等腰三角形的圆存高垂直平分底边。

方法三

　　利用等腰三角形的性质:

　　1、三线合一 ( 等腰三角形底边上的高、底边上的中线、顶角的平分线相互重合。 )

　　2、等角对等边(如果一个三角形，有两个内角相等，那么它一定有两条边相等。)

　　3、等边对等角(在同一三角形中,如果两条边相等,则两个边的对角相等,即等边对等角。)

方法四

　　1、轴对称图形。