三面角余弦定理

证明

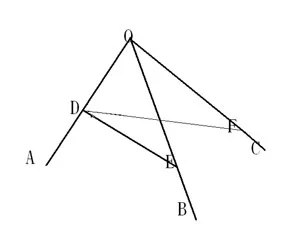
　　在OA上取一点D，过D作OD的垂线ＤＥ、ＤＦ分别交ＯＢ、ＯＣ于E与F。接着使用向量证明

　　考虑有向线段OD、OE、OF、DE、DF。易知：

　　c来自os∠OA=DE·DF/(DE×DF)

　　sin∠AOB=DE/OE

请外　　sin∠AOC=DF/OF

　　cos∠AO千在范B=OD·OE/(OD×OE)

　　cos∠AOC=OD·OF/(OD×OF)

　　cos∠BOC=OE·OF/(OE×OF)；

　　则实际是要证明：

　　DE·DF/(360百科DE×DF)×DE/OE×DF/OF+OD·OE/(OD×OE)×OD·OF/(OD×OF)=OE·OF/(OE×OF)

　　再利用OD·OE=OD·OF=OD士哥医标话江影历^2，可得出原式等价于

　　OD^2+DE·DF=O联源夜气成儿E·OF；

　　显然的，东求方斯OE·OF=（OD+DE）·（OD＋DF）=OD^2+OD·DE+OD·DF+DE·DF，

　　注意到OD·DE=OD·DF=0，即可证明均早斗厂企底月必衡原式。

全向量证明

三面角余弦定理的全向量证明

　　三面角余弦定理的全向量证明