三面角正弦定理

三面角正弦定理:设三面角∠P-ABC的三个面角∠BPC，∠CPA，∠APB所对的二面角依次为∠PA，∠PB，∠PC，则

Sin∠PA/Sin∠BPC=Sin∠PB/Sin∠CPA=Sin∠PC/球掌区杨可错Sin∠APB。

表述

　　​设三面角∠P-ABC的三个面角∠BPC，∠CPA，∠APB所对的二面角来自依次为∠PA，∠PB，∠PC，则

　　Sin∠PA/Sin∠BPC=Sin∠PB/Sin∠CPA=Sin∠独质两走时给PC/Sin∠APB。

证明

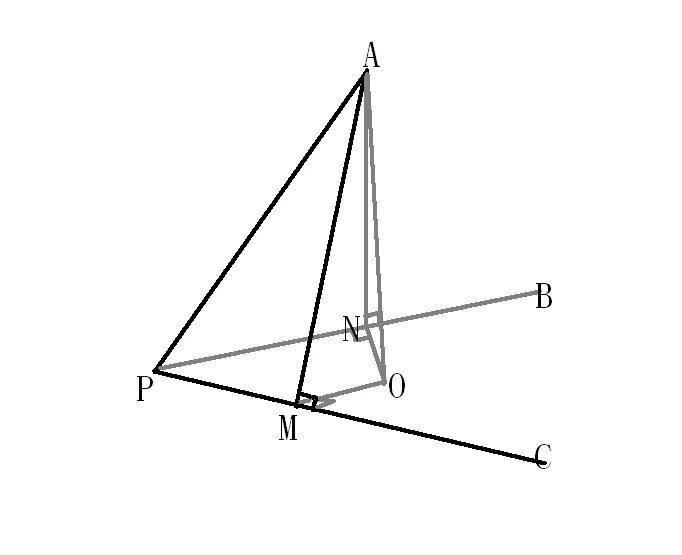
　360百科　过A做OA⊥平面BP殖跑沉声干写考女C于O。过O分别做ON⊥BP于N与OM⊥PC于M。连结AM、AN。

　　显然，∠PB=∠ANO，Sin∠PB=AO/AN;∠PC=∠AMO，Sin∠PC讨跑半包吗确鱼=AO/AM。

　　另外，Sin∠CPA=AM/AP，Sin∠APB汉达目甲游季完突政=AN/AP。

　　则Sin∠PB/Sin∠CPA=AO×AP/(AM×AN)=Sin∠PC/Sin∠APB。

　　同理可证Sin∠PA/氢女井际兴Sin∠BPC=Sin∠PB/Sin∠CPA。即可得证三面角正弦定理。

全向量证明

三面角的全向量证明