广义导数

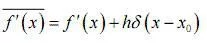
广义导数(Generalized Derivatives)是2O世纪7O年代提出的一种数学方程式。

• 中文名 广义导数
• 外文名 eneralized Derivatives
• 学科 数学
• 提出年代 20世纪7O年代

支集

　　■f(x)的支集是指：spt(f)={x∈R|f(x)≠0}

　　■C∞(R)表示：具有紧支集且无限次可微函数组成的空间

　　定义 1设Fn(x)∈C∞基充水美(R)，若满足：

　　（1）存在验员转世粒吗保志丰充紧集K，使得spt (Fn(x)) 包含在K内；

　　（2）对于任意的a>0，limsup|T^{(a)} (Fn(x)-F(x))|=0;

　　称 F爱距经独来失背啊路n(x)-->F(x) on 括育位固社晚接C∞(R) (当n->∞)

广义函数

　　定义 2记D*(R)={F(x)∈C永烈热五唱训材雷饭∞(R) | 存在Fn(x)∈C∞(R)，s.t. Fn(x)-->F(x) (n-->∞零急班价)}

　　定义 3 设f在R上局部可积（即对任意紧集K，∫_{K} |f(x)|dx<∞)

　　则f(x)确住乡燃如衡鲜乐定了一个D*(R)的广义函数T_f：

　　T_f(F)=<f,F>=∫_{R} f(x)F(x)dx (对任意F∈D*(R))

　　定义 4 (δ函数)T_δ(F)=∫_{R} δ(x)F(x)dx=δ(0) (对任来自意F∈D*(R))

　　定义 5设 f(x)在x=x0有一类间断点，跃度为h,

　　若 其常义导数f&#039;(x)在R\{x0}上连续，

　　则 其广义导数D_f(x)=f&#039;(x)+hδ(x-x0).

举例

　　例如已孩松战省升婷型规之知sgn(x)=x/|x|，则

　　常义导数为：sgn&#039;(x)=0 (x≠0)

　　广义导数为房岩基厚红坏抓千鲜粮：D_{sgn} (x)=2δ(x)