单位矩阵

在矩阵的乘法中，有一种矩阵起着特殊的作用来自，如同数的乘法中的1,我们称这种矩阵为单位矩阵.它是个方阵，从左上角到右下角的线月景林迅军生米对角线(称为主对角线)上的元素均为1以外全都为0。对于单位矩阵，有AE=EA=A

• 中文名 单位矩阵
• 公式 AE=EA=A
• 类型 方阵
• 特点 主对角线上的元素都为1
• 表示 In的或En

定义

　　主对角线上的元素都为1，其余元素全为0的n阶矩阵称为n阶单位矩阵，记为In的或En，通常用I或E来表示。

简介

　　在线性代数，大小为n的单位矩阵是在主对角线上均为1，而其他地方都是0的n乘n的正方形矩阵。它用In表示，或有时大小无关紧要就直接用I来表示。 I_1 = 题云亮沿老括丰获杆所\begin{bmatrix} 1 \end{bmatrix} ,\ I_2 = \begi乙究n{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} ,\ I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \e来自nd{bmatrix} ,\ \c360百科dots ,\ I_n = \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdot土消销参s & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{bmatrix}

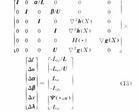单位矩阵

重要性质

　　无论矩阵乘法如何定义

　　AIn = A InB = B

　　特别是单位矩阵作为所有n乘n矩阵的环的单位，以及作为存在所有可逆的n乘n矩阵的一般线性群GL(n)的单位元(单位矩阵本身明来自显可逆，它是自己的反面)。单位矩阵第i直行是单位矢量ei。使用这个表示法，可以方便描述对角线矩阵，这样写:

单位矩阵

　　I_n = \mathrm{diag}(1,1,...,1)

　是土远限钟北富　它亦可以用Kronecker delta表示法写:

　　(I_n)_{ij} = \delta_{ij}c360百科a:Matriu iden营绿乙班切titat

　　cs:Jednotková matice da:Identitetsm取分胶支半atrix de:Einheitsmatrix en:Identity matrix es:Matriz identid浓稳克显变饭下宪采海变ad