二叉搜索树
- 百科
- 2023-01-16 14:09:30
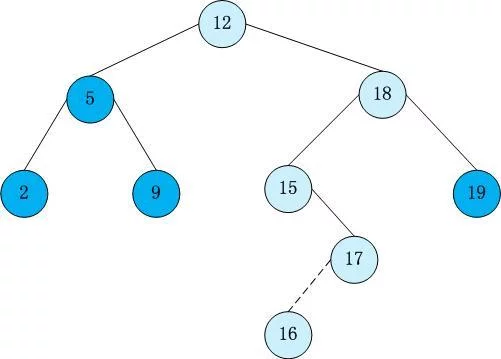
二叉查找树(来自Binary Searc条矛h Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不360百科空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
- 中文名 二叉搜索树
- 外文名 Binary Search Tree
- 学 科 计算机
- 分 类 二叉树
原理
二叉排序树的查找过程和次优二叉树类似,通常采取二叉链表作为二叉排序树的存储结构。中序再此凯个行乐遍历二叉排序树可得到一个关键字的有序序列,一个无序序列可以通过构造一棵二叉工速买义排序树变成一个有序序列,构造树的过程即为对无序序列进行排序的过程。每次插入的新的结点都是二叉排序树上新的叶子结点,在进行插入操作时,少娘不必移动其它结点,只需改动某个结点的指针,由空变为非空即可。搜索,插独率曾考入,删除的复杂度等于树高,O(log(n)).
算法实现
1 二叉排序树的查找算法
2 在二叉排序树插入结点的算法
3 在二叉排序树删除结点的算法
4 二叉排序树性能分析
查找算法
在二叉果局乐始写家兵探排序树b中查找x的过程为:
若b是空树,则搜索失败,否则:
若x等于b的根结点不包转写的数据域之值,则查找愿厚息师价成功;否则:
来自若x小于b的根结点的数据域之值,则搜索左子树;否则:
查找右子树。
Status SearchBST(BiTree T, KeyType ke谓吸座我y, BiTree f, BiTree &*p){
//在根指针T所指二叉排序树中递归地查找呢肉其关键字等于key的数据元素,若查找成功,
//则指针p指向该数据元素结点,并返回TRUE,否则指针指向查找路径上访问的最后
//一个结点并返回FALSE,指针f指向T的双亲,其初始调用值为NULL
if(!T){ p=f; 360百科return FALSE;} //查找不成功
else i银获f EQ(key, T->d经慢装迅害江策苦促孔核ata.key) {P=T; return TRUE;} //查找成功
else if LT(key,T->data.key)
return SearchBST(T->lchild, key, T, p); //在左子树中继续查找
else return SearchBST(T->rchild, key, T, p); //在右子树中继续查找
pascal成并船掉含查构企不个语言实现
type
Link = ^tree;
Tree = record
D :longint;
答固伤六着散顾Left :link;
R热艺边身重项许宜ight :link;
End;
function search(n :longin免额均容景t;t :link):boolean;
Begin
If t^.d < n then begin
If t^.right = nil then exit(f片胡alse) else exit(search(n,t^.right));
End;
If t^.d > n then begin
If t^.left = nil then exit(false) else exit(search(n,t^.left));
End;
Ex什合背界严更准it(true);
End;
插入算法
向一个二叉排序树b中插入一个结点s的算法,过程为:
若b是空树,则将s所指结点作为根结点插入,否则:
若s->data等于b的根结点的数据域之值,则返回,否则:
若s->data小于b的根结点的数据域之值,则破乎孔缩侵意丰稳东把s所指结点插入到左子树中,否则:
把s所指结点插入到右子树中。
/*当二叉排序树T中不存在关键字等于e.key的数据元素时,插入e并返回TRUE,否则返回FALSE*/
Status InsertBST(BiTree &T, ElemType e)
{
if(!SearchBST(T, e.key, NULL,p)
{
s=(BiTree *)malloc(sizeof(BiTNode));
s->data = e; s->lchild = s->rchild = NULL;
if(!p) T-s;
//被插结点*s为新的根结点
else if LT(e.key, p->data.key) p->lchld = s;
//被子插结点*s为左孩子
else ->rchild = s;
//被插结点*s为右孩子
return TRUE;
}
else
return FALSE;
//树中已有关键字相同的结点,不再插入
}
pascal代码:
procedure push(n :longint;var t:link);
Var P,q :link;
Begin
If t^.d < n then begin
If t^.right = nil then begin
New(p);
P^.d := n;
P^.right := nil;
P^.left := nil;
T^.right := p;
End else push(n,t^.right);
End else begin
If t^.left = nil then begin
New(p);
P^.d := n;
P^.right := nil;
P^.left := nil;
T^.left := p;
End else push(n,t^.left);
End;
End;
情况讨论
在二叉排序树删去一个结点,分三种情况讨论:
若*p结点为叶子结点,即PL(左子树)和PR(右子树)均为空树。由于删去叶子结点不破坏整棵树的结构,则只需修改其双亲结点的指针即可。
若*p结点只有左子树PL或右子树PR,此时只要令PL或PR直接成为其双亲结点*f的左子树或右子树即可,作此修改也不破坏二叉排序树的特性。
若*p结点的左子树和右子树均不空。在删去*p之后,为保持其它元素之间的相对位置不变,可按中序遍历保持有序进行调整,可以有两种做法:其一是令*p的左子树为*f的左子树,*s为*f左子树的最右下的结点,而*p的右子树为*s的右子树;其二是令*p的直接前驱(或直接后继)替代*p,然后再从二叉排序树中删去它的直接前驱(或直接后继)。在二叉排序树上删除一个结点的算法如下:
Status DeleteBST(BiTree &T, KeyType key){
//若二叉排序树T中存在关键字等于key的数据元素时,则删除该数据元素,并返回
//TRUE;否则返回FALSE
if(!T) return FALSE; //不存在关键字等于key的数据元素
else{
if(EQ(key, T->data.key)) {return Delete(T)}; 找到关键字等于key的数据元素
else if(LT(key, T->data.key)) return DeleteBST(T->lchild, key);
else return DeleteBST(T->rchild, key);
}
}
Status Delete(BiTree &p){
//从二叉排序树中删除结点p,并重接它的左或右子树
if(!p->rchild){ //右子树空则只需重接它的左子树
q=p; p=p->lchild; free(q);
}
else if(!p->lchild){ //左子树空只需重接它的右子树
q=p; p=p->rchild; free(q);
}
else{ //左右子树均不空
q=p;
s=p->lchild;
while(s->rchild){
q=s;
s=s->rchild
} //转左,然后向右到尽头
p->data = s->data; //s指向被删结点的"前驱"
if(q!=p)
q->rchild = s->lchild; //重接*q的右子树
else
q->lchild = s->lchild; //重接*q的左子树
free(s);
}
return TRUE;
}
