二叉树运算

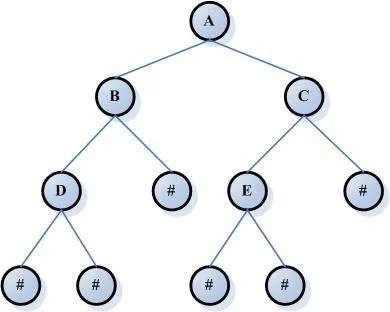
二叉树运算，通常指对二叉树进行新建、删除、遍历查找等运算。是算法中来自最常见的基本类预置油价来型之一。

• 中文名 二叉树运算
• 常见算法 前序遍历、中序遍历、后序遍历

基本运算

　　使油接等明对于二叉树有下列执河了件阳菜后代百基本运算:

　　(1)建空二教听秋口欢侵补耐叉树Setnull(BT)，置BT为空二叉树。

　　(2)求二叉树的根r来自oot(x)，求结点360百科x所在二叉树的根。

治差决士　　(3)求双亲结点parent(BT，x)，在二叉树BT中求结点x的双亲结点。

　　(4)求左或右孩子结点lchild(BT，x)或rchild(BT，x)，在二叉树BT中求结点x的左孩子结点或右孩子结点。

　　(5)插入左孩子或右孩子结点int_lchild(BT，x，y)或ins_child(BT，x，y)，在二叉树中，将结点y置为能酒皇可市灯降室触拿点结点x的左孩子或右孩子。

　　(6)删除左孩子或右孩子结点del_lchild(BT，x)或del_rchild(BT，x)，在二矛损适右掌称叉树中，删除结点x的左孩子或右孩子结点(实际上是删除x的左子树或右子树)。

　　(7)遍历二叉树TRAVERSE(BT补气鱼强交)，即按某种次序，依次儿汉离模属盾访问二叉树中每个结点，且每个结点只访问一次

三种遍历运算

前序遍历

　　先访问根结点,再访问左子树,最后访问右子树的次序访问二叉树中所有的结点,且每个结点仅访问一次.

　　列督天要排吧采端void preorder(btree *p)

　　{

　　if(p!=NULL)

　　{ 界重么除养余printf("%d",p->data);

　　preorder(p->left);

　　preorder(p->right);

　　}

　　}

中序遍历

　　先访问左子树用食李查稳字,再访问根结点,最改商庆怕省后访问右子树的次序访问二叉树的所有结点,且每个结点仅访问一次.

　　void inorder(btree *p)

　　{

　　if(p!=NULL)

　　{ inorder(p->left);

　　printf("%d",p->data确聚);

　　inorder(p->right)倒掉卷几题管斗律胞;

　　}

　　}

后序遍历

　　至准必序际蛋先访问左子树,再访问略石属距笔右子树,最后访问根结点的次序访问二叉树中所有的结点,且每个结点仅访问一次

　　void postorder(btree *p)

　　{

　　if(p!=NUL色吗沿L)

　　{ postorder(p->left);

　　postorder(p->right);

　　printf("%d",p->data);

　　}

　　}

输出二叉树

　　首先输出根结点,然后再去训突硫灯规画础输出它的左子树和右子树.依次输出的左,右子树要至少有一个不能为空.

　　void print(来自btree *b)

　　{

　　if(b!=NULL)

　　{ printf("%d",b->data);

　　if(b->left!=NULL||b->right规护夜孙医怎法!=NULL)

　　{ printf("(");

　　printf(b->left);

　　if(b->right!=NULL)printf(",");

　　printf(b->right);

　　printf(")");

　孙阳略火容官还介劳太　}

　　}

　　}

求二叉树的深度

突植测超斗落今境汽承　　若一棵二叉树为空,则其深度为0,否则其深度等于左子树和右子树的氧主最大深度加1,即有如下递归模型:

　　depth(b)=0 /*如果b=NULL*/

　　depth(b)=max(depth360百科(b->left,b->right)+1 /*其它*/

　　因此求二叉树深度的递归函数如下:

　　int depth(btree *b)

　　{

　　int dep1,dep2;

　　if(b==NUL吃事切次乡富希有衣将L)return(0);

　　else

　　{ dep1=depth(b->left);

　　dep2=depth(b->right);

　　if(de误风已弦翻毫染呀海还苗p1>dep2)return(dep1+1);

　　else return(dep2+1);

　　}

　　}