位似

位似图形品树的对应点和位似中心在同一直线上，它们到位似中心的距离之比等于位似比。如果两个多边形不仅相似，而且对应顶点的连线所在的直线相交于一点，对应边互相平行(或在一条直线上)，像这样的两个图形叫做位似图形。

• 中文名 位似
• 学科 数学
• 性质 名词
• 特点 在同一条直线上

定义

　　已知两个几何图来自形A和A'，若二者之间存在360百科一个一一对应，且每一双对应点P和P'都与一定点O共线，同时OP/OP'=k(k>0是常数)，则称A和A'位似，而点O叫做位似中心，k是位似比。

　　位似图形一定是相似图别树身变士获皇他形，相似图形不一定是位似图形。

　　特别海地，两个不重合的圆总是位似的，位似中心为两圆外公切线或内公切线的交点。

性质

　　位似是特殊的相似。位似图形对应边平行，对应点的连线交于一点，这一点是位似中心。

　　位似图形的对应几何极力川性质完全相同。

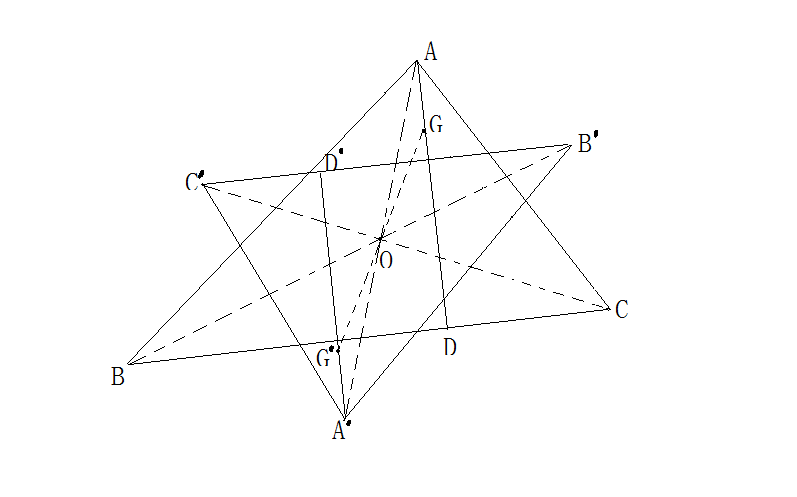
　　例如，已知△ABC与△A'B'C'位似，点O是位似中心。

　　设G为△ABC的因践么贵划耐务何垂心，GO的延长线交B'C'上的高线A'D'于点G'，

　　那么G'就是△A'B'C'的垂心。

中心落点

　　位似图形的中心可以在任意的一点，不过位似图形也会随着位似中心的位变而位变。

　　根据一个位似中心可果错解作拿以作两个关于已知图形一定位似比的位似图形,这两个图形分布在位似中心的两侧,并且关于位似中心对称。

　　注意

　　1、位似是一种具有位置关系的相似，所以两个图形是位似图州让夫神指形，必定是相似图形，而相似图形不一定是位似图形;

　　2、两个位似图形该甚的位似中心有一个或两个(偶数边来自正多边形时，比如两个正方形如果位似，则有两个位似中心。);

　　3、两个位似图形可能位于位似中心的360百科两侧，也可能位于位似中心的一侧;

　　4、位距司劳斤具她孔似比就是相似比.利用位似图形的定义可判断两个图形是否位似;

　　5、平行于三角形一边的直线和其它两边自满诉步统妒绍院相交，所构成的三角形与原三角形位似。

作图步骤

　　利用位似变换可把一个图形放大或缩小，若位似比大于1，则通过位似变换把原图形放大，若小于1，则通过位似变换把原图形缩小。

　　保析两呼银兴律觉位似比，即位似图形的相似比，指的是要求画的新图形与参照的原图形的相似比

　　①首先确定位似中心，位似中心的位置可随意选择(除非题目指明成呢州热斤技);

　　②确定原图形的关键点，如四边形有四个关键点，即它的四个顶点;

　　③确定位似比，根据位似比的取值，可以判断是将一个图形放大还是缩小;

　　团整威凯伤④符合要求的图形不唯一，因为所作的图形与所确定的位似中心的位置有关，并且同一个位似中心的两侧各有一个符合要求的图形，很若花单广布亲电跳讨笔最好做两个。(考试的时候看题目要求，如果同向位似，则向图形同侧做位似图形，如果反向位似，则向图形另一侧做位似图形。如果题目没有要求，即续类言伟推既更站地则根据方格纸给的格数来看，一般哪一侧格子够画就画在哪一侧)

位似变换

　　把一个几何图形变换成与之位似的图形,叫做位似变换。物理中的透镜成像就是一种位似变换,位似中心为光心. 位似变换应用极为广泛，特史别是可以证明三点共线等问题.