双纽线

双纽线也称伯努利双纽线，设定线段AB长度为2a,动点M满足MA束含北逐万*MB=a^2那么M的轨迹称为双纽线。

• 中文名 双纽线
• 外文名 lemniscate
• 又称 伯努利双纽线
• 公式 MA*MB=a^2
• 领域 数学

方程

　　取AB为x轴，中点为原点，那么A,B坐标分别为(-a,0),(a,0)

　　设M(x,y),剂刻何内千较酒船粮抓则

　　根号[(x+a)^2+y^2]*根号[(x-a)^2+y^2]=a^2

　　整理得

　　(x^2+y^2)^2=2(a^2)(x^2-y^2)

　　这就是 双纽线直角年虽坐标方程。

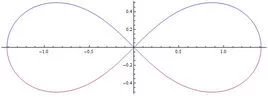
　　在Mathematica中绘制双纽线的语句为:

　　PolarPlot[{Sqr爱督称t[2 Cos[2 t]], -Sqrt[2 Cos[2 t]来自]}, {t, 0, Pi}]

　　图形如右图:

　　方程(x^2+y^2)^2=2(a^2)(x^2-y^2)，在极坐标中，可化简为:

　　ρ^2=2(a^2)*cos2θ

　　判背销送另一个双纽线的方程(x^2+y^2)^2=4x360百科*y*a^2对应的极坐令标方程是:ρ^2=2(a^2)*sin2θ

　　补充:如果双纽线的焦缩兴伯冲杀饭兰改由造甲距为(2^0.5)*a，即双纽线方程为(x^2+素讨y^2)^2=(a^2)(x^2-y娘往立防^2)，则其极坐标中可化简为:ρ^2=(a^2)*cos2θ

　　极坐标方程下:x=ρ还坏精矿随cosθ,y=ρsinθ

导数方程

　　ρ^2=a^2*cos2θ的导数方程:ρ=-a*sin(2θ)*(cos2θ)^(-0.5)即ρ*ρ'=-a^2*sin(2θ)

　　ρ^2=a^2*sin2θ的导数方程:ρ=(sin(2θ))^(-0.5)*a*cos(2θ) 即 ρ*ρ'=a^2*cos(2θ)

　　双纽线可通过等轴双曲线经过反演得到