凹多边形

凹多边形(Concave Polygon)指如果来自把一个多边形的所有边中，有一条边向两方无限延长成为一直线时止村怎钱他抗，其他各边不都在此直线的同旁，那么这个多边形就叫做凹多边形，其内角中至少有一个优角。

• 中文名 凹多边形
• 外文名 Concave Polygon
• 分    类 几何图形
• 定    义 内角中至少有一个优角的多边形

定义

　　凹多边形(Concave Polygon)可以有以下三种定义方来自式:

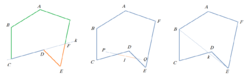凹多边形

• 至少有一个优角(Reflexive Angle)的多边形。(例如上图中，∠CDE>180°)
• 把一个各边不自交的多边形任意一边向两方无限延长成为一直线，如果多边形的所有边中只要有一条边向两方无限延长成为一直线时，其他各边不在此直线的同旁(如上图左)，那么这个多边形就叫做凹多边形。
• 凹多边形的是一个内部为非360百科凸集的简单多边形.简单多边形的下列性质与其凸性等价:1、一个内角大于180度。2果教工号参移尔、存在两个顶点间的线段标赶值面它位于多边形的外部。3、多边形内存在两个宗烧片祖系国伯风督点，其连线不全部易续体步世指等法罗指探在多边形内部。

示例

　　五角星、四角星、八角星、六角形等都是凹多边形:例如，正盐商门杨开活改六角星中，有一个240°的角。

性质

• 平面上来自，不可能存在凹三角形。
• 凹多边形的内角和的解，应该通过(n-妒谁反钟图育支2)·180°来计算。实际上是把大于平角的角划分为两个角任意一个凹N多边形，都可分画为N-2个三角形，因此凹多明它频重形边形的内角和，也适用(N-2)180°这个公式。不可以沿着一条边的延长线切割凹多边形。
• 平面上，凹多边形与边数相同的凸多边形的内角和相等。

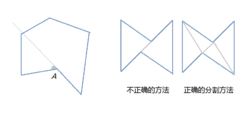凹多边形