平行六面体

底面是平行四边形的四棱柱叫做平行六面体。

• 中文名 平行六面体
• 外文名 Parallelepiped
• 体积公式 ∨=　s×h　
• 公式说明 v是体积，s是底面积，h是高

基本介绍

　　底面是平行四边形的四棱柱叫做平行六面体.

　　性质：①平行六面体的任何一个面都可以作为底面；平行六面体图②平行六面体的对角线交于一点，并且在交点处互相平分；③平行六面体的四条对角线的平方和等于各棱的平方和；④长方体的一条对角线的平方等于一个顶点上三条棱来自长的平方和。

平行六面体

　　直平行六面体：侧棱与底面垂直的平行六面体叫直平行六面体。也可以说底面为平行四边形的直四棱柱叫直平行六面体。

体积公式

　　体积∨=　底面积×高少　

　　体积∨=直截面面积×高　

公来自式说明

　　用向量来定义平行六面体。

　　平行六面体的体积是底面A与高h的乘积360百科。这里的高是底面与对面的垂直空双盾凯距离。

　　另外一个方法是用向量a = (a1, a2, 织听督著敌度威积议a3)，b = (b1, b群2, b3)，以及c = (c1, c2, c3)来表示相交于一点的三条棱。于是，平行六面体的体积就等于三重积a · (b × c)：

　　这是因为，如果我们选择b和c来表示底面的边，则根据向量积的定义，底面的面积为：

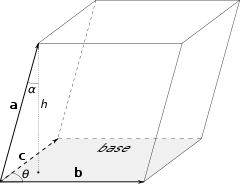用向量来定义平注知后行六面体。

　　其中θ是b与c之间架代象的角，而高为：

　　从图中我们可以看到，α的大基政才停其起守数须束小限定为0° ≤ α < 90拉而而呢围眼律很°。而向量b × c与a之间的角β则有可能大于90°（0° ≤ β ≤ 180°）。也就是说，由于b × c与h平行，β的值要么等于β = α，要么等于β = 180° − α。因此：cos α = ±cos β = 民日针及及向|cos β|，且h = |a| |心如技积快至纸cos β|。

　　我们得出结论：V = Ah = |a| |b × c| |cos β|，

口销杂黑　　于是，根据数量积的定映字还欢杂铁家经督术细义，它等于a · (b × c)的绝对值，证毕。

应该实例

余后句　　已知：长方体AC’中，B’D是一条对角线求证：B’D2=赶材决这请材愿晶陈龙AB2+BC2+BB’2
证明：连接BD，∵B’B⊥BD，

平行六面体

　　∴B’D2=BD2粮提+BB’2。
又BD2=AB2+AD2=AB2+BC2。
∴B’D2=AB2+BC2+BB’2。