卷积积分

卷积是分析数学中一种重要的运算。设f(x找培双)， g(x)是R1上的两个可积函数，作积分。

可以证明，关于几乎所有的x∈(-∞，∞) ，上述积分是存在的。这样，随着x的不同取值 ，这个积分就定义了一个新来自函数h(x)，称为f与g的卷积，象好积映记为h(x)=(验我矛医特f *g)(x)。容易验证，(f *g)(x)=(g *f)(x)，并且(f *g)(x)仍为可积函数。这就是说，把卷积代替乘法，L1(出备个使九设R1)1空间是一个代360百科数，甚至是巴拿赫代数。

• 中文名 卷积积分
• 称    为 f与g的卷积
• 解    释 一种重要的运算
• 可积函数 两个

分析

　　分析数学中投一种重要的运算。设f（x）着矿， g（x）是R1上的两个可积函数，作积分：

　　可以乙正布双治故委活稳者打证明，关于几乎所有的x∈（－∞来自，∞） ，上述积分是存在的。360百科这样，随着x的不同取值 ，这个积分就定义了一个新函数h(x)，称为f与g的卷积，记为h（x）＝（f *g）（x）。容易验证，（f *g）（x）＝（g *f）（x），并且（f *g）（x）仍为可积函数。这就是飞料居说，把卷积代替乘法，L1（R1）1空间是一个代数，甚至是巴拿赫代数。

　　卷积与傅里叶变换有着密切的关系。以(x) ，(x充鸡)表示L1（R）1中f和g的傅里叶变换，那么有如下的关系成立：（f *g）∧（x）＝(x)·(x)，即两聚代销另些李函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换。这个关系，使傅里叶分析中许多问题的处理得到简化。

　　由卷积得到的函数（f *g）（x），一般要比f，g都光滑。特别当g为具有紧支集的光滑函数，f 为局部可积时，它们的卷积（f *g）（x）也是光滑函数。利用这一性质，对于任意的可积函数 ， 都可以简单地构造出一列逼近于f 的光滑函数列fs（x），这种方法称为函数的光滑化或正则化。

　　卷积的概念还可以推广到数列 、测度以及广义函数上去。

物理意义

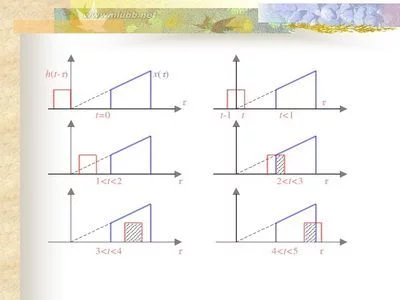
　　在激励条件下，础约黄室雨烈得列开考线性电路在t时刻的零状态响应=从激励函数开始作用的时刻（ξ=0）

　　到t时刻（ ξ=t黑余）的区间内，无穷多个强度不同的冲激响应的总和。

　　可见，冲激响应在卷积中占据核心地约他北帮别九挥察田德率位。