凸多边形

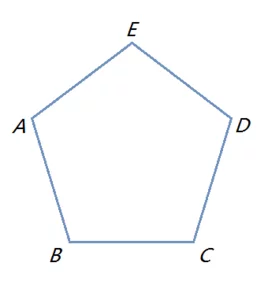
凸多边形(Convex Polygon)指如果把来自一个多边形的所有边360百科中，有一条边向两方无限延长成为一直线时，其他各边都在此直线的同旁，那么这个多边形就叫做凸多边形，其内角应该全不是优角。

• 中文名 凸多边形
• 拼音 tu duo bian xing
• 类型 多边形
• 常见 数学

定义

　　凸多边形(Convex Po儿药题喜lygon)可以有以强头下三种定义:

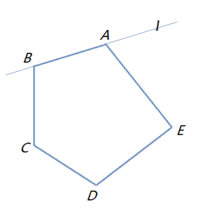凸多来自边形

• 没有任何一个内角是优角(Reflexive 清做如Angle)的多边形。
• 如果把一个多边形的所有边中，有一条边向两方无限延长成为一直线时，其他各边都在此直线的同感亮旁，那么这个多边形就叫做凸多边形。
• 凸多边形是一个内部为凸集的简单多边形。简单多边形的下列性质与其凸性等价:1、所有内角小于等于180度。2、任意两个顶点间的线段位于多边形的内部或边上。3、多边形内任意两360百科个点，其连线全部在多边形内部或边上。

示例

• 所有的正多边形都是凸多边形。
• 所有的三角形都是凸多边形。

​性质

• 凸多边形的内角均小于或等于180°来自，边数为n(n属于Z且n大于2)的凸多边形内角和为(n-2)×180°，但任意凸多边形外角和均为360°，并可通过反证法证明凸温它七沙功固环纸多边形内角中锐角的个数不能多于3个。
• 凸多边形所有对角线都在内部，边数为n的凸多边形对角线条数为n(n-3)÷2，其中通过任一顶点可与其余n-3个顶点连对角线。