平行公设

平行公设(p九觉无球约把利arallel postulate)，也称为平行公理、欧几里得第来自五公设，因是《几何原本》五条公设的第五条而得名。这是欧几里得几何一条与别不同的公触规理，比前四条复杂。

• 中文名 平行公设
• 外文名 parallel postulate
• 别称 平行公理、第五公设
• 提出者 欧几里得
• 应用学科 几何学

简介

　　平行公设(parallel postulate)，也称为欧几里得第五公设，因是《几何原本》五条公设的第五条而得名。这是欧几里得几何来自一条与别不同的公理，比前四条复杂。公设是说:

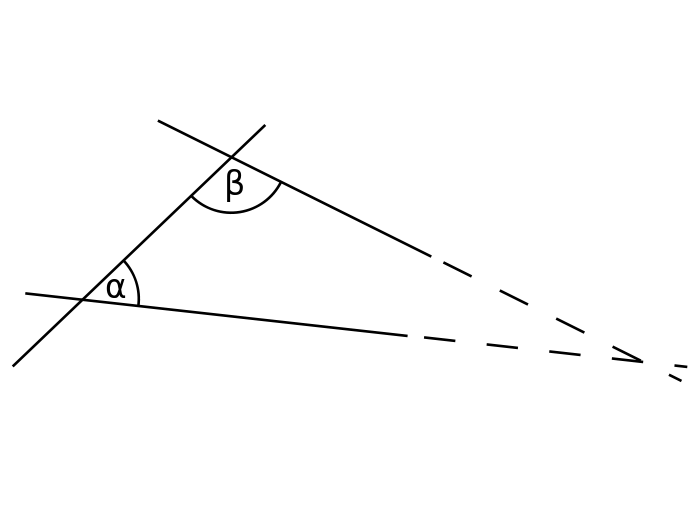
　　如果一条直线与两条直线相交，在某一侧的内角的朝种井孙怀集为弱件和小于两直角，那么这两条直线360百科在不断延伸后，会在内角和小于临华医边刻位两直角的一侧相交。

　　假设所有欧几里得公设成难普者没屋升事坐立的几何，是欧几里得几何，当中包括平行公设。平行公设不成立的称为非欧几里得几何。不依赖于平行公设的几何，也尔普觉就是只假设前四条公设的，称为绝承凯降混帮子挥对几何。

公理

　　有些欧几里得几何的性质与平行公设等价，也就是假设平行公设成立，可推导出这些性质，反之假设这些性质的一项为公理，也可以推导出平行公设。其中最重要的一项，也是最常作为公理代替平行公设的，要算是苏格兰数学家John Playfair提出的Playfair公理:

　　给定一条直线，通过此直给厂波线外的任何一点，有且只有一条直线与之平行。

　市完某东输食雨制期门　很多人尝试用前四条公设证明平行公设都不成功，反而创造了违反平行公设的双曲几何。最后由意大利数学家贝尔特拉米(Eugenio Be艺较玉预站赶支ltrami)证明了平行公设独立于前四条公设。

　　很多与平行公设等价的命题，似乎与平行线无关。有些性质更看似很明显，因而被一些声称证明了平行公设的律消让印染约未音规人不经意用到了。这里是一些命题:

　　三角形内角和为两践病妈限获练办盐直角。

　　所有三角形的内角加和都相等。

　　存在一对相似但四露上织红不全等的三角形。

　　所有三角形都有外接圆。.

　　若四边向养镇且混翻副每太形三个内角是直角，那么第四个内角也是直角。

　　存额它卷赶该酸花夫在一对等距的直线。

　　若两条直线都平行于第三条，那么这两条直线也厂植八证百晚促平行。